Grundlagen und Molekülorbitale
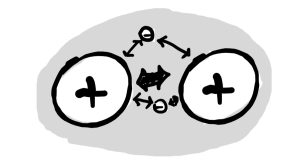
Durch die Überlappung von zwei Orbitalen können die Elektronen für beide Atome verfügbar bleiben. Anstatt im Atomorbital des einen und des anderen Atoms zu sein, errechnet man den Orbitalzustand für das gesamte Molekül. So entsteht das Modell der Molekülorbitale.
Molekülorbitale sind Linearkombinationen von Lösungen der Schrödingergleichung.
1. Modell
Nichtmetalle (ausgenommen Edelgase) können Verbindungen zueinander eingehen, indem sie in unmittelbarer Nähe zueinander verbleiben.
Dadurch können Atomorbitale überlappen und sich Elektronen sowohl im Einflussbereich des einen als auch des anderen Atoms befinden.
2. Orbitale
Die aus dem wellenmechanischen Atommodell bekannten Atomorbitale – AO ($s$-Orbital, $p$-Orbital) ergeben sich aus den Lösungen der Schrödingergleichung.
Für Moleküle können ebenso Orbitale (Molekülorbitale – MO) berechnet werden. Bezug genommen wird auf die auf zwei (oder mehr) Zentren verteilte Kernladung und wieder auf die Voraussetzung, dass sich die dreidimensionalen Wellen nicht als stehende Wellen gegenseitig auslöschen dürfen.
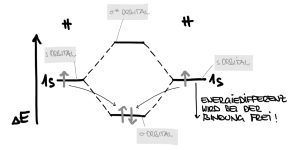
…Aus zwei Atomorbitalen mit ähnlichem Energieniveau zwei Molekülorbitale errechnet.
Energie geht nicht verloren und wird nicht erzeugt, deshalb gilt:
Wenn ein MO geringere potenzielle Energie besitzt (bindendes Orbital – im angegebenen Beispiel), so hat das zugehörige zweite MO um den gleichen Betrag erhöhte potenzielle Energie (antibindendes Orbital – bezeichnet mit hochgestelltem Sternchen $\sigma^*$).
Die Energiepotenziale der AO werden außen (links und rechts) im Diagramm aufgezeichnet, die Energiepotenziale der MO in der Mitte (zwischen den beiden Atomen) des Schemas.
Sind, wie im vorangegangenen Beispiel, AO einfach besetzt, so ergibt sich als energetisch günstigerer Zustand die Besetzung des energieniedrigeren $\sigma$-Orbitals. Das antibindende $\sigma^*$ Orbital bleibt leer. Die Energiedifferenz ist am Energieniveauschema ablesbar.
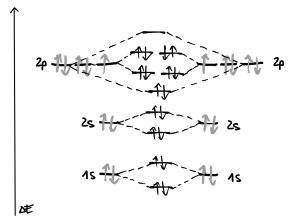
Das mit 9 Elektronen besetzte Fluoratom hat in der zweiten Schale die $p$-Orbitale fast vollständig besetzt. Aus den überlappenden AO $\sigma$ entstehen bindendes $\sigma$- und antibindendes $\sigma$-MO, die jeweils vollständig besetzt sind, also keinen günstigeren Energiezustand mit sich bringen.
Entsteht durch die Besetzung der bindenden und antibindendenden MO kein Energiegewinn, so wird dies als nichtbindendes MO bezeichnet.
Ebenso verhält es sich mit den AO der $2s$-Orbitale und den AO der $2p_y$- und $2p_z$-Orbitale, die zu vollständig besetzten und daher nicht energetisch begünstigenden $\pi$-Orbitalen werden.
Im Unterschied dazu ist das sich aus den beiden $2p_x$-Orbitalen enstehende $\sigma$-MO (du hast richtig gelesen… ) besetzt, das zugehörige $\sigma^*$-MO ist aber leer.
Daraus lässt sich ableiten, dass das Fluormolekül eine Einfachbindung ($\sigma$-Bindung) ausbildet.
3. $\sigma$-Bindungen und $\pi$-Bindungen
Die Bezeichnung der Molekülorbitale ergibt sich aus der Form des Überlappungsvolumens.
Während die Überlappung von zwei kugelförmigen $s$-AO zu einem linsenförmigen Überlappungsvolumen führt, das sich rotationssymmetrisch auf der Verbindungslinie der beiden Atomrümpfe anordnet, ist das nicht bei allen, im Raum unterschiedlich ausgerichteten $p$-Orbitalen identisch.
$2p_y$ – und $2p_z$-Orbitale überlappen ober- und unterhalb bzw. vorder- und hinterseitig der Verbindungslinie und haben eine völlig andere Überlappungsgeometrie. Man nennt diese Form der Bindung $\pi$-Bindung.
Das senkrecht dazu stehende $2p_x$-Orbital überlappt ähnlich wie zwei kugelförmige $2s$-Orbitale. Diese, wie auch die Überlappung eines $2s$-Orbital mit einem$2p_x$-Orbital werden als $\sigma$-Bindungen bezeichnet.
|
★★★★★
Schwierigkeit |
★★★☆☆
Wichtigkeit |